What is pH – pH Scale Definition
pH refers to the concentration of hydrogen ions in solution. The lower the pH the more hydrogen
ions present. The higher the pH the fewer hydrogen ions present
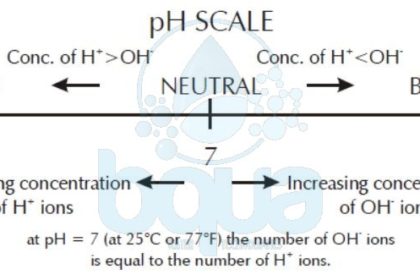
pH scale: Concentration of Hydrogen ions
The acidity and alkalinity of a solution is extremely important in Reverse Osmosis water treatment due to factors such as membrane degradation, membrane cleaning, etc. This is because certain chemical reactions will only take place at specific pH values.
The term pH is used to describe whether a solution is alkaline or acidic. The concept of acidity and alkalinity may best be described by going back to the dissociation constant.
Looking at the exponent on the concentration of Hydrogen H+ ion, we see that as the H+ concentration goes up (and OH- concentration goes down) we get a smaller negative number. Likewise, as Hydroxide OH- concentration goes up (and H+ concentration goes down) we get a larger negative number.
[H+] x [OH-] = 1.0 x 10^-14
With addition of acid (H+)
1.0 x 10^-5 x 1.0 x 10^-9 = 1.0 x 10^-14
With addition of base (OH-)
1.0 x 10^-9 x 1.0 x 10^-5 = 1.0 x 10^-14
Exponent changes with changes in H+ and OH- concentrations
Taking this into consideration, scientists learned that a more convenient way to describe the hydrogen ion concentration of a solution is to take the negative logarithm of the hydrogen ion concentration. A logarithm is the exponent to which a base number is raised to produce a given number. NOTE: We will usually use a base of 10.
EXAMPLE: The log (logarithm) of 100 is 2: Ten raised to the power of 2 (102).
EXAMPLE: The log of 127 is 2.1 (On a scientific calculator, enter 127, then push the [LOG] key).
| NUMBER | LOG | NUMBER | LOG |
| 1 = 1 X 10^0 | 0 | 1.0 = 1 X 10^0 | 0 |
| 10 = 1 X 10^1 | 1 | 0.1 = 1 X 10^-1 | -1 |
| 100 = 1 X 10^2 | 2 | 0.01 = 1 X 10^-2 | -2 |
| 1000 = 1 X 10^3 | 3 | 0.001 = 1 X 10^-3 | -3 |
| 10000 = 1 X 10^4 | 4 | 0.0001 = 1 X 10^-4 | -4 |
| 100000 = 1 X 10^5 | 5 | 0.00001 = 1 X 10^-5 | -5 |
| 1000000 = 1 X 10^6 | 6 | 0.000001 = 1 X 10^-6 | -6 |
| 10000000 = 1 X 10^7 | 7 | 0.0000001 = 1 X 10^-7 | -7 |
The symbol for the negative log is “p”. Therefore, the negative log of the Hydrogen ion concentration is “pH”. Table below lists several hydrogen ion concentrations, hydroxide concentrations, and the corresponding pH and pOH. Note that a pH of 7 is neutral because the Hydrogen ion concentration [H+] and hydroxide concentration [OH-] are the same. As [H+] increases, pH decreases.
| H+ (mol/L) | OH- (mol/L) | ||||
| Decimal | SN | pH | Decimal | SN | pOH |
| 0.00000000000001 | 1 X 10^-14 | 14 | 1.0 | 1 X 10^0 | 0 |
| 0.0000000000001 | 1 X 10^-13 | 13 | 0.1 | 1 X 10^-1 | 1 |
| 0.000000000001 | 1 X 10^-12 | 12 | 0.01 | 1 X 10^-2 | 2 |
| 0.00000000001 | 1 X 10^-11 | 11 | 0.001 | 1 X 10^-3 | 3 |
| 0.0000000001 | 1 X 10^-10 | 10 | 0.0001 | 1 X 10^-4 | 4 |
| 0.000000001 | 1 X 10^-9 | 9 | 0.00001 | 1 X 10^-5 | 5 |
| 0.00000001 | 1 X 10^-8 | 8 | 0.000001 | 1 X 10^-6 | 6 |
| 0.0000001 | 1 X 10^-7 | 7 | 0.0000001 | 1 X 10^-7 | 7 |
| 0.000001 | 1 X 10^-6 | 6 | 0.00000001 | 1 X 10^-8 | 8 |
| 0.00001 | 1 X 10^-5 | 5 | 0.000000001 | 1 X 10^-9 | 9 |
| 0.0001 | 1 X 10^-4 | 4 | 0.0000000001 | 1 X 10^-10 | 10 |
| 0.001 | 1 X 10^-3 | 3 | 0.00000000001 | 1 X 10^-11 | 11 |
| 0.01 | 1 X 10^-2 | 2 | 0.000000000001 | 1 X 10^-12 | 12 |
| 0.1 | 1 X 10^-1 | 1 | 0.0000000000001 | 1 X 10^-13 | 13 |
| 1.0 | 1 X 10^-0 | 0 | 0.00000000000001 | 1 X 10^-14 | 14 |